Since I started trading, I have seen many posts saying that each chartist figure like « Double Bottom » gives a success rate greater than 80%! With some success, I traded double-bottom figures in weekly and monthly time frames. However, my results have not been near as promised. This post will present the real success rate of double bottoms to help you better operate this trading strategy. I will show you an algorithm capable of shape recognition, and run backtests on the Prorealtime platform.

- What is a double bottom?
- How to recognize a double bottom using an algorithm?
- Double bottom indicator
- Create a chartist bot
- The success rate of the double-bottom
- How to improve the performance of the double-bottom algorithm?
- Limitations and bias of this study
- What I think about chartist figures
- How to improve a trading system?
What is a double bottom?
The double bottom is one of the most known chartist figures by traders. It is a figure that looks like the « W » letter. It is considered a bullish reversal. This chartist figure is mainly used to operate technical rebound in the short-term perspective or to open middle-term entry in the case of a recovery trading strategy.
How to recognize a double bottom using an algorithm?
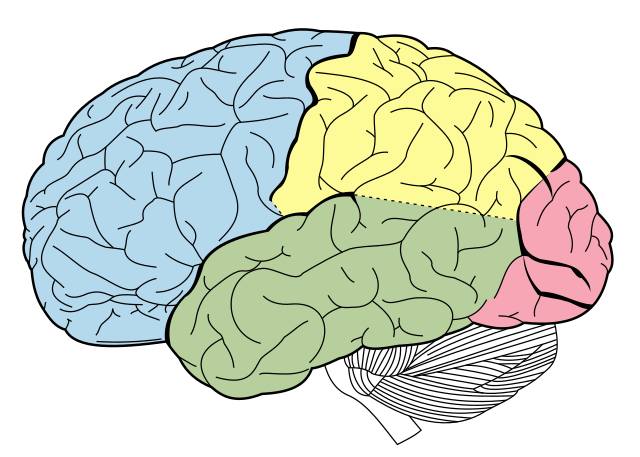
The visual recognition of things is as wide and exciting in algorithmics. The human brain is exceptionally gifted in recognizing shapes. You are capable of recognizing any object around you at first glance. The occipital cortex supports the cognitive processing of visual recognition at your brain’s back. The occipital lobe represents 18% of your brain and is almost exclusively reserved for image processing and understanding!
I will leave you to imagine the needed number of code lines and computing power to reproduce this part of human capacity using an algorithm or artificial intelligence.
Don’t panic, there is a tip!
Luckily, there will always be some algorithm or trick to help us solve a problem. First, we can reduce the problem-space to recognizing one alone object in a given context.
For this example, I will show you an algorithm allowing recognition of only the double bottom shape with a width of ten candles. That will be sufficient to make some tests and get the first conclusions. Besides, since we work on two dimensions, that is to say, the price and the time, the complexity will be reduced, making the processing easier.
Recognizing a shape thanks to a little mathematic trick
If you remember your school mathematics courses, you have undoubtedly heard about correlations at least once. They allow comparing two curves to know if they vary simultaneously. If two curves, c1 and c2, are correlated, they vary simultaneously. That means if c1 increases, then c2 also increases; if c1 decreases, then c2 decreases. That is precisely what you need to recognize a chartist figure. You will calculate the correlation between a chartist figure and the market price movement. If the price is correlated with the chartist figure, this figure probably appeared.
Double bottom recognition source code
You need to process two steps to recognize a double bottom. You have to describe the shape in a table and then calculate the correlation with the price. To simplify this example, I artificially created an elementary double-bottom figure. I drew a W letter in an Excel sheet starting with a price equal to ten and a width of ten candles.
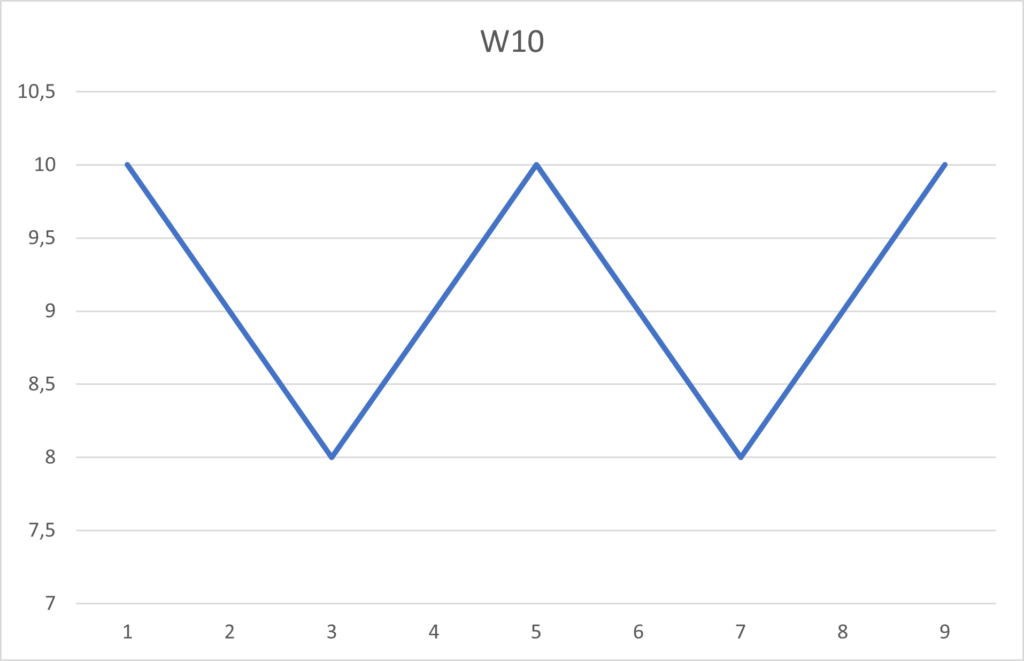
Description of the double bottom figure in a table
The table expressing the double bottom figure is the following: [10, 9, 8, 9, 10, 9, 8, 9, 10]. Now, you have to code it in the Prorealtime platform.
// Chartist Figure to recognize
$x[0] = 10
$x[1] = 9
$x[2] = 8
$x[3] = 9
$x[4] = 10
$x[5] = 10
$x[6] = 9
$x[7] = 8
$x[8] = 9
$x[9] = 10
Comparison between the price and the chartist figure
Now, you must compare the similarity between this double bottom and the price movement. To make this comparison, you need to compute the correlation between the ten points of the previous table and the last ten candles. If the correlation is greater than 0.80, you can consider that a double bottom occurred:
xBar = 0
FOR i = 0 TO lastset($x) DO
xBar = xBar + $x[i] / period
NEXT
varianceX = 0
FOR i = 0 TO lastset($x) DO
varianceX = varianceX + SQUARE($x[i] - xBar) / period
NEXT
ecarTypeX = SQRT(varianceX)
$y[0] = Close[9]
$y[1] = Close[8]
$y[2] = Close[7]
$y[3] = Close[6]
$y[4] = Close[5]
$y[5] = Close[4]
$y[6] = Close[3]
$y[7] = Close[2]
$y[8] = Close[1]
$y[9] = Close[0]
yBar = Average[period](Close)
ecarTypeY = STD[period](Close)
covarianceXY = 0
FOR i = 0 TO lastset($x) DO
covarianceXY = covarianceXY + (($x[i] - xBar) * ($y[i] - yBar)) / period
NEXT
// Coeficient de correlation
R = covarianceXY / (ecarTypeX * ecarTypeY)
The correlation coefficient will be contained in the R variable in the previous code.
Double bottom indicator
Now, you have all that is necessary to succeed in the creation of a double bottom indicator for the Prorealtime platform. You have to add a boolean condition that will be true when the correlation coefficient is greater than a threshold. In principle, it is admitted that two curves are correlated when the correlation coefficient is greater than 0.8.
Double bottom indicator source code
This is the source code of the double-bottom indicator. To implement it on the Prorealtime platform, you have to open the indicator interface, copy-paste the code, and run the execution.
//W10.INDICATOR
ONCE period = 10
ONCE threshold = 0.8
R = 0
$x[0] = 10
$x[1] = 9
$x[2] = 8
$x[3] = 9
$x[4] = 10
$x[5] = 10
$x[6] = 9
$x[7] = 8
$x[8] = 9
$x[9] = 10
xBar = 0
FOR i = 0 TO lastset($x) DO
xBar = xBar + $x[i] / period
NEXT
varianceX = 0
FOR i = 0 TO lastset($x) DO
varianceX = varianceX + SQUARE($x[i] - xBar) / period
NEXT
ecarTypeX = SQRT(varianceX)
$y[0] = Close[9]
$y[1] = Close[8]
$y[2] = Close[7]
$y[3] = Close[6]
$y[4] = Close[5]
$y[5] = Close[4]
$y[6] = Close[3]
$y[7] = Close[2]
$y[8] = Close[1]
$y[9] = Close[0]
yBar = Average[period](Close)
ecarTypeY = STD[period](Close)
covarianceXY = 0
FOR i = 0 TO lastset($x) DO
covarianceXY = covarianceXY + (($x[i] - xBar) * ($y[i] - yBar)) / period
NEXT
// Correlation coefficient
R = covarianceXY / (ecarTypeX * ecarTypeY)
// Double Bottom detection
IF R >= threshold AND R < 1 THEN
w10 = 1
ELSE
w10 = 0
ENDIF
RETURN W10 AS "W10"
In the previous example, if the value of the R variable is greater than 0.8, the algorithm will send a double bottom detection signal. I also added a condition that checks R is lower than 1. For specific reasons to temporal series treatment, data misses some candles. In this case, the correlation coefficient could be greater than 1. This result is a mathematical error because the correlation coefficient must be between -1 and 1.
Automatic double bottom detection example
Here is an example of a double bottom detection thanks to the previous chartist indicator ran on the Prorealtime platform:
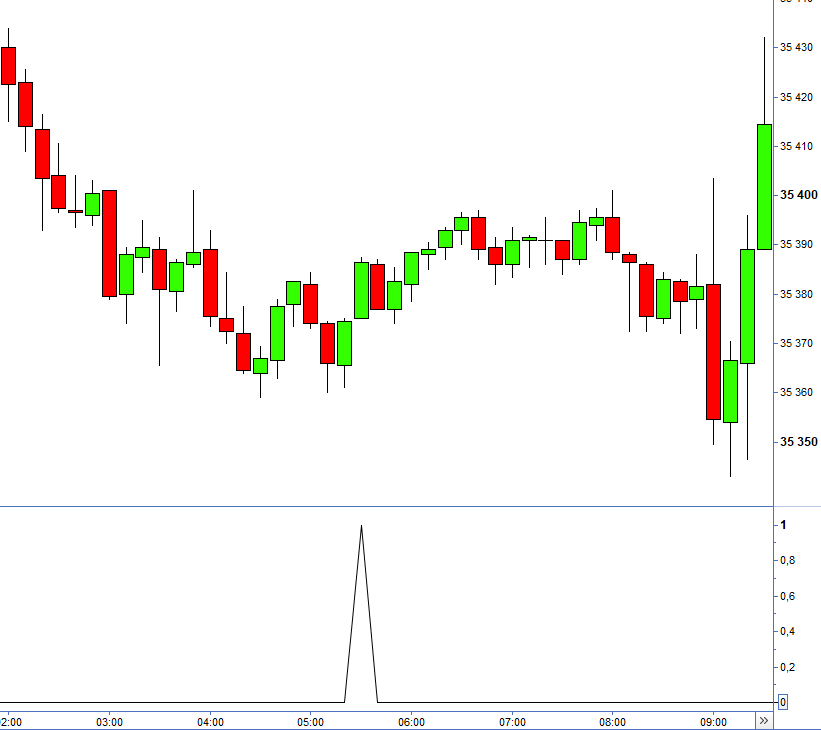
Create a chartist bot
You will easily create a chartist bot using the previous source code of the double bottom indicator. This trader bot can open a long entry after a double bottom occurs in the market. To simplify the code, I will statically place the stop loss at 80 points and the target at 160 points.
I prefer that the robot is awake only during the market cash session for security reasons. That means the trader bot will be only active from 09h00 until 21h30. (I considered the starting European session until the end of the American session)
Source code of Double bottom bot
//--------------------------------------------------------------------------
// W10.STRATEGY.DOW.10M
// AUTOR: Vivien Schmitt
// https://artificall.com
// THIS STRATEGY MUST BE RUN ON THE DOW JONES WITH A "10-minutes" TIMEFRAME
//--------------------------------------------------------------------------
DEFPARAM CUMULATEORDERS = false // only one trade in the same time
DEFPARAM FLATBEFORE = 090000 // avoide entry opening before this hour
DEFPARAM FLATAFTER = 213000 // close entry at this hour
//--------------------------------------------------------------------------
ONCE period = 10
ONCE threshold = 0.8
R = 0
//--------------------------------------------------------------------------
$x[0] = 10
$x[1] = 9
$x[2] = 8
$x[3] = 9
$x[4] = 10
$x[5] = 10
$x[6] = 9
$x[7] = 8
$x[8] = 9
$x[9] = 10
xBar = 0
FOR i = 0 TO lastset($x) DO
xBar = xBar + $x[i] / period
NEXT
varianceX = 0
FOR i = 0 TO lastset($x) DO
varianceX = varianceX + SQUARE($x[i] - xBar) / period
NEXT
ecarTypeX = SQRT(varianceX)
//--------------------------------------------------------------------------
$y[0] = Close[9]
$y[1] = Close[8]
$y[2] = Close[7]
$y[3] = Close[6]
$y[4] = Close[5]
$y[5] = Close[4]
$y[6] = Close[3]
$y[7] = Close[2]
$y[8] = Close[1]
$y[9] = Close[0]
yBar = Average[period](Close)
ecarTypeY = STD[period](Close)
covarianceXY = 0
FOR i = 0 TO lastset($x) DO
covarianceXY = covarianceXY + (($x[i] - xBar) * ($y[i] - yBar)) / period
NEXT
//--------------------------------------------------------------------------
R = covarianceXY / (ecarTypeX * ecarTypeY)
IF R < threshold OR R > 1 THEN
R = 0
ENDIF
//--------------------------------------------------------------------------
conditionW10 = R
//--------------------------------------------------------------------------
// OPEN A LONG ENTRY
IF NOT LongOnMarket AND conditionW10 THEN
PSTOPLOSS = 80
PTARGET = PSTOPLOSS * 2
SET STOP pLOSS PSTOPLOSS
SET TARGET pPROFIT PTARGET
BUY 1 CONTRACT AT MARKET
ENDIF
The success rate of the double-bottom
You will finally discover the real success rate of the double-bottom trading strategy. To get it, you have to run a backtest of the previous code and check the result:
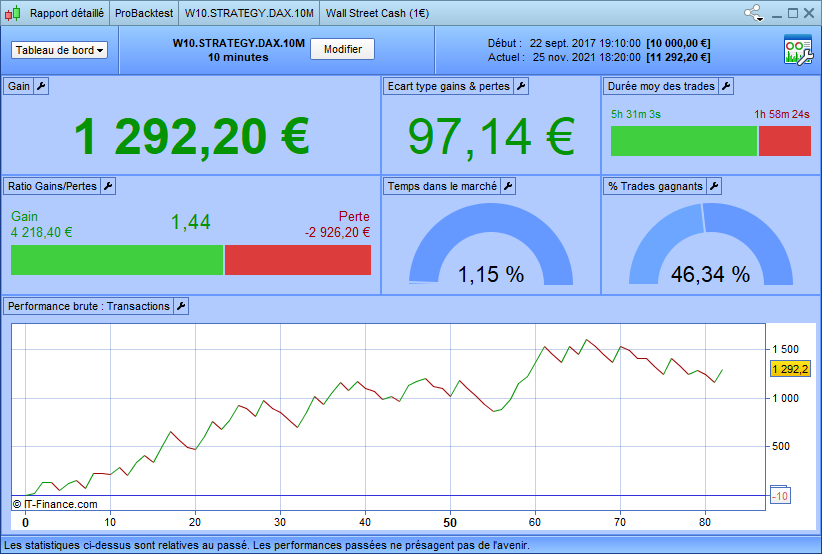
Together with you, I am surprised by the result! The last time I conducted this study, the success rate was near 55%. This result is far from the 80% announced by most trading blogs!
How to improve the performance of the double-bottom algorithm?
You probably heard about the neckline if you have already traded double bottoms. I will try to improve the performance of this chartist trading system by implementing neckline management.
What about the double bottom neckline?
The neckline of a double bottom figure is the highest price reached by the double bottom top. It is a kind of short-term resistance.
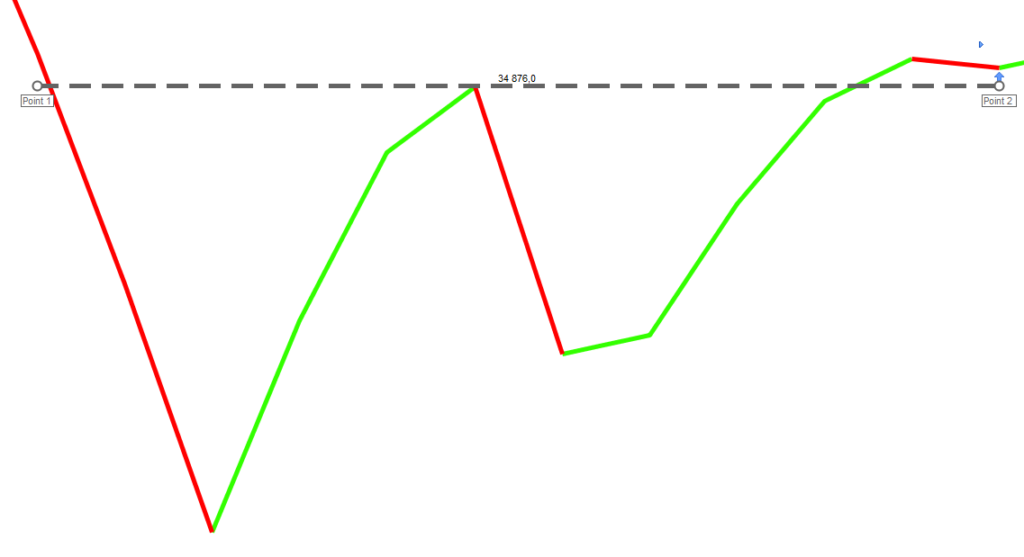
The equation of the neckline is relatively simple: it corresponds to the highest price reached on the x candles corresponding to the figure width. In this example, the double bottom width is ten candles.
I will add a condition that will become true if the price closes above the double bottom neckline.
neckline = close => highest[10](close)Source code of Double bottom bot with neckline
I needed to add a delay of one candle after the double bottom condition to implement the neckline in the algorithm. I added this delay to allow the market to close above the neckline just after the double bottom.
The following trading system will open an entry only if a double bottom appears and if the price closes above the neckline:
//--------------------------------------------------------------------------
// W10.STRATEGY.DOW.10M
// AUTOR: Vivien Schmitt
// https://artificall.com
// THIS STRATEGY MUST BE RUN ON THE DAX INDEX WITH A "10-minutes" TIMEFRAME
//--------------------------------------------------------------------------
DEFPARAM CUMULATEORDERS = false // only one trade in the same time
DEFPARAM FLATBEFORE = 090000 // avoide entry opening before this hour
DEFPARAM FLATAFTER = 213000 // close entry at this hour
//--------------------------------------------------------------------------
ONCE period = 10
ONCE threshold = 0.8
R = 0
//--------------------------------------------------------------------------
$x[0] = 10
$x[1] = 9
$x[2] = 8
$x[3] = 9
$x[4] = 10
$x[5] = 10
$x[6] = 9
$x[7] = 8
$x[8] = 9
$x[9] = 10
xBar = 0
FOR i = 0 TO lastset($x) DO
xBar = xBar + $x[i] / period
NEXT
varianceX = 0
FOR i = 0 TO lastset($x) DO
varianceX = varianceX + SQUARE($x[i] - xBar) / period
NEXT
ecarTypeX = SQRT(varianceX)
//--------------------------------------------------------------------------
$y[0] = Close[9]
$y[1] = Close[8]
$y[2] = Close[7]
$y[3] = Close[6]
$y[4] = Close[5]
$y[5] = Close[4]
$y[6] = Close[3]
$y[7] = Close[2]
$y[8] = Close[1]
$y[9] = Close[0]
yBar = Average[period](Close)
ecarTypeY = STD[period](Close)
covarianceXY = 0
FOR i = 0 TO lastset($x) DO
covarianceXY = covarianceXY + (($x[i] - xBar) * ($y[i] - yBar)) / period
NEXT
//--------------------------------------------------------------------------
R = covarianceXY / (ecarTypeX * ecarTypeY)
IF R < threshold OR R > 1 THEN
R = 0
ENDIF
//--------------------------------------------------------------------------
neckline = close => highest[period](close)
//--------------------------------------------------------------------------
conditionW10 = R
//--------------------------------------------------------------------------
// OPEN A LONG ENTRY
IF NOT LongOnMarket AND conditionW10[1] AND neckline THEN
PSTOPLOSS = 80
PTARGET = PSTOPLOSS * 2
SET STOP pLOSS PSTOPLOSS
SET TARGET pPROFIT PTARGET
BUY 1 CONTRACT AT MARKET
ENDIF
Performance of the double bottom bot implementing the neckline
This is the new performance of the double-bottom trading system that opens entries only if the price closes above the neckline:
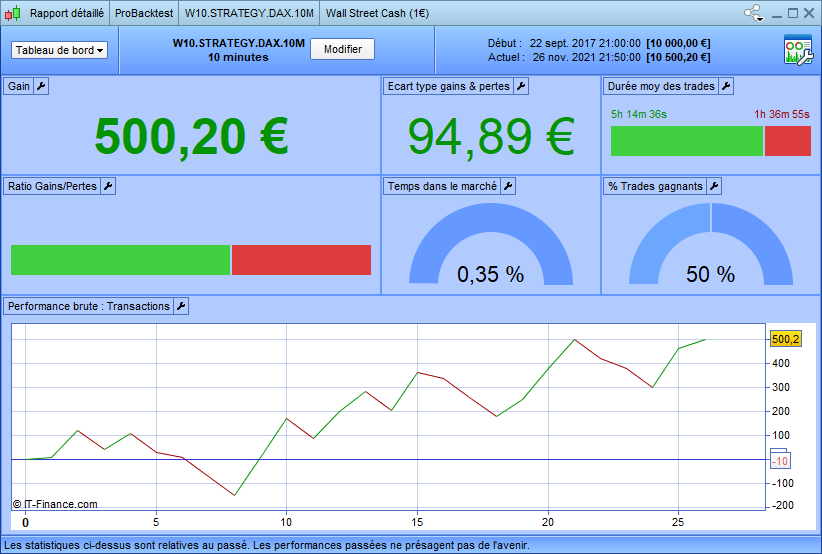
You can see that the algorithm’s performance strongly decreased. However, three essential properties have evolved: the number of openings is significantly lower, the success rate is 50%, and the risk-reward ratio has increased.
Limitations and bias of this study
As in all market studies, some statistical biases and limitations impact the final result. These are the two main biases of this study:
1. Limitation of the chartist recognition algorithm
The first bias comes from the algorithm I used to recognize the double bottom figure. This algorithm is built on correlations and gives some results but is constrained. It only allows the recognition of chartist figures having a fixed width. In addition, this algorithm tends to trigger false positives. What happens in particular when data miss candles on the chart?
2. Stop loss and target positionings
In this study, I placed the stop loss and the target statically. The stop loss and the target have systematically been placed at 80 points and 160 points, respectively. Habitually, when you trade chartist figures, you should set the stop loss and the target depending on the figure’s height.
What I think about chartist figures
I operated chartist figures many times in the past. I traded them manually with a weekly swing trading strategy and automatically with a day trader bot. I gradually disengaged from chartist strategies to move toward trend-following strategies. Today I consider that the trend-following strategy is simpler and gives more return than the chartist strategy. However, my chartist experience influences me when I watch a chart. That helps me sometimes to avoid traps and optimize my long-term investment entries.
How to improve a trading system?
In the next post, I will present how to improve the return of an automated trading system with very few code lines. I will show you how to reduce losing entries while avoiding the overfitting risk.
If not, I encourage you to discover my other articles in the free learning section.
Don’t hesitate to give me your opinion about the chartist figures and share your feedback on your experience. I’d be delighted to respond. 😊
Range Breakout Indicator for Prorealtime [FREE]
The Range Breaker will help you seize the best trading opportunities. It detects range breakouts, which are often followed by explosive movements. Thanks to this indicator, you will never miss a breakout again.
Sources and credit images
Head image: https://www.maxpixel.net/Alphabet-Gold-W-Gradient-Abc-Letter-Lowercase-146063
Brain image: https://en.wikipedia.org/wiki/Occipital_lobe
Occipital proportion: https://faculty.washington.edu/chudler/facts.html